Jul 2012
Removing unreliable structure
05/07/12 10:25
I want to build a classifier for sounds, but I’d like to pre-process the images to remove unreliable structure. Is this possible?
Answer:
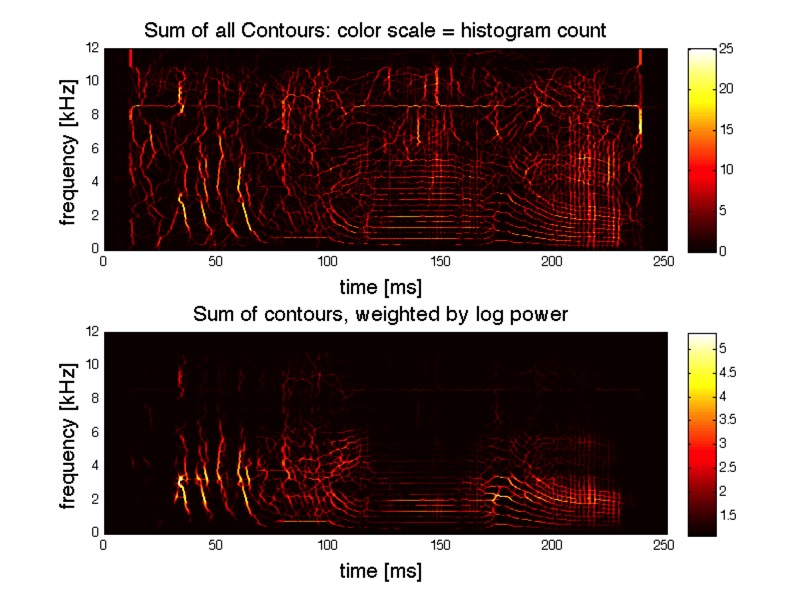
Time-frequency microstructure is unstable for regions of the time-frequency plane with spectrally dense content. For those regions, small changes in analysis parameters or added background noise in the signal can lead to changes in the details of a sonogram or contour shapes. Structurally unstable portions of the representation can be eliminated by showing only contour fragments that are in agreement across different angles and time-scales of analysis.
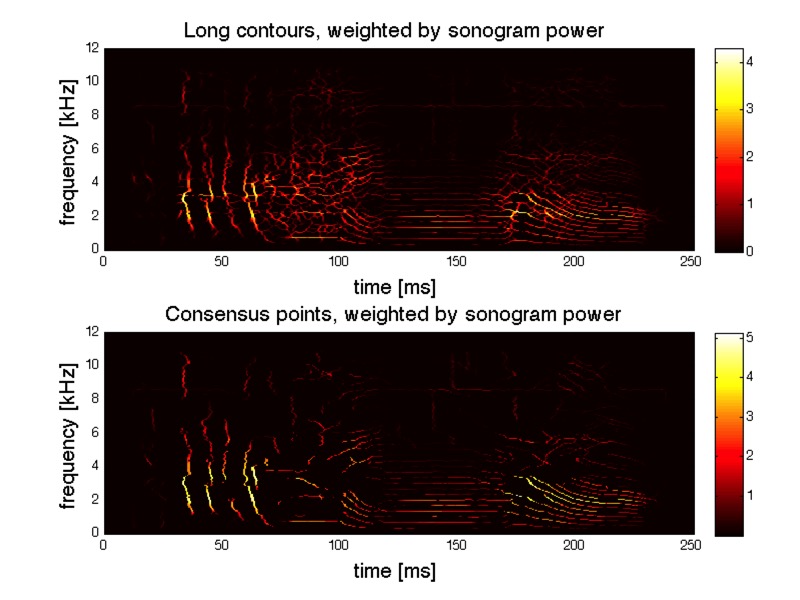
The image below illustrates that process. On top, all long contours are shown, weighted by sonogram power.
On bottom, only the structurally stable “consensus” elements are shown, also weighted by sonogram power.
Answer:
Time-frequency microstructure is unstable for regions of the time-frequency plane with spectrally dense content. For those regions, small changes in analysis parameters or added background noise in the signal can lead to changes in the details of a sonogram or contour shapes. Structurally unstable portions of the representation can be eliminated by showing only contour fragments that are in agreement across different angles and time-scales of analysis.
The image below illustrates that process. On top, all long contours are shown, weighted by sonogram power.
On bottom, only the structurally stable “consensus” elements are shown, also weighted by sonogram power.

Does the result reflect true signal?
04/07/12 12:03
At the outset, every part of the signal is represented many times over using different time scales and angles.
Signal components are then filtered out if they are too small, or not structurally stable. This filter parameter allows the result to scale continuously from a representation that is complete to a representation that captures only the most salient features. We are now working on a script to quantify how much of the signal has been left out at a given filter setting.
Since the image combines contours from many time-scales and angles, aspects of a signal can be represented more than once. (See the discussion on Glottal Pulses and Harmonic stacks.)
Signal components are then filtered out if they are too small, or not structurally stable. This filter parameter allows the result to scale continuously from a representation that is complete to a representation that captures only the most salient features. We are now working on a script to quantify how much of the signal has been left out at a given filter setting.
Since the image combines contours from many time-scales and angles, aspects of a signal can be represented more than once. (See the discussion on Glottal Pulses and Harmonic stacks.)
Glottal Pulses and Harmonic stacks
04/07/12 10:31
The harmonic stacks show funny vertical lines or clicks: are those real?
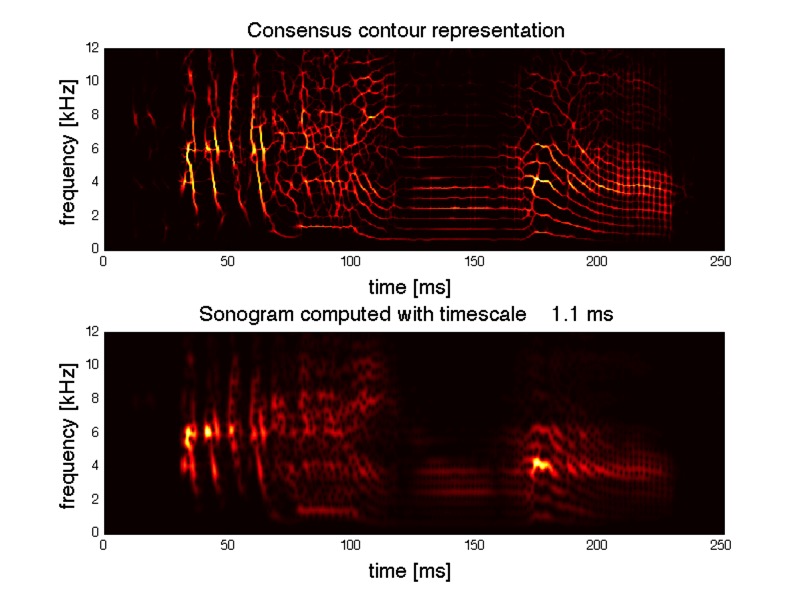
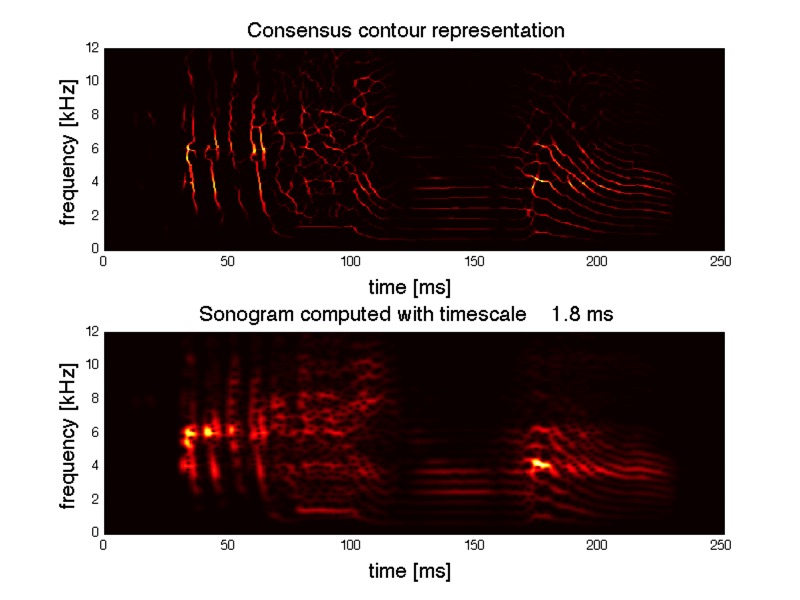
Answer: The clicks in the harmonic stacks can appear when short time scales are included in the analysis.
In the first image below, the timescale was .5-2ms. The clicks are the glottal pulses, and intervals between the clicks equals the fundamental frequency.
The second image is calculated without the shorter time-scales, using timescales 1.5-2ms. The glottal pulses disappear.
Answer: The clicks in the harmonic stacks can appear when short time scales are included in the analysis.
In the first image below, the timescale was .5-2ms. The clicks are the glottal pulses, and intervals between the clicks equals the fundamental frequency.
The second image is calculated without the shorter time-scales, using timescales 1.5-2ms. The glottal pulses disappear.


What are the essential steps in the algorithm?
01/07/12 11:20
The method first computes contours for many time-scales and angles. The edges of the contours are derived from a generalization of reassigned sonograms, and share similarities with spectral derivatives. Edges are grouped together to form objects with a definite beginning and end. Each contour has an associated waveform. The sum of all contour waveforms for a given time-scale and angle provides a perfect representation of any signal. Since every time-scale and angle provides a complete representation of the sound, the collection of all contours is over-complete.
Shown next are contours for a single time-scale, and two specific angles.
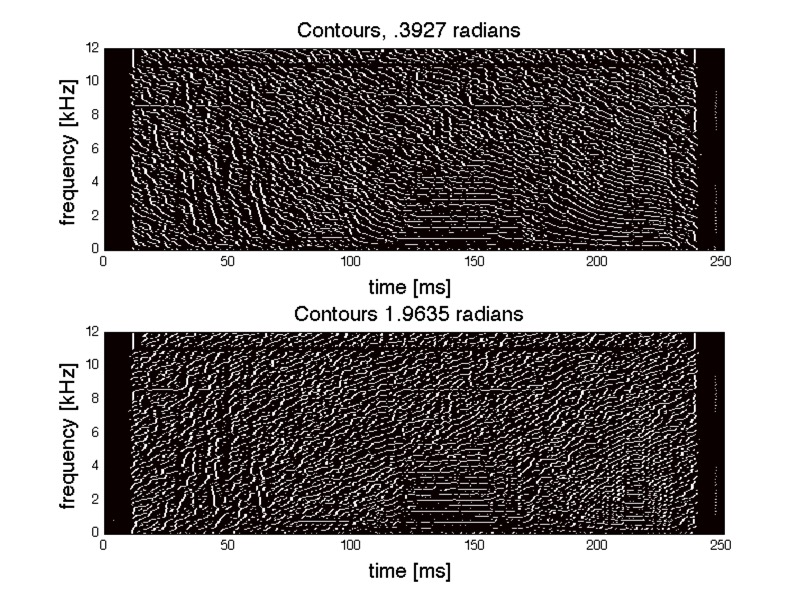
Next, contours shorter than some percentile are discarded. (98 percentile in the next image.)
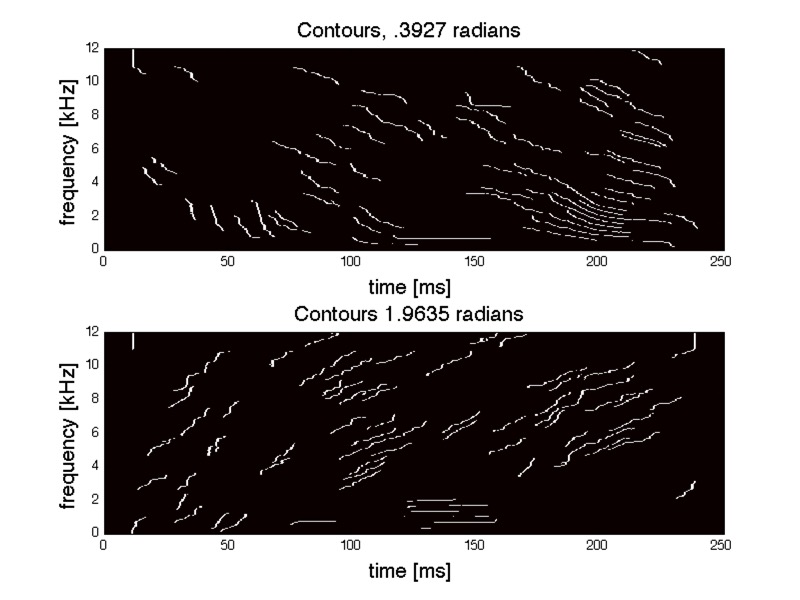
Then, all long contours from all angles and all time-scales are added together. The binary contours can be added to produce a two-dimensional histogram (top image), or weighted by local power in the time-frequency plane (bottom). In the latter case, each contour is weighted by the sonogram computed in the same time-scale as the contour.