Lab 2 of Part 1:
Stochastic Systems
Key concepts
A.
State space form of linear
difference equation
B.
Stochastic simulation: a
recursive approach
C.
Impulse response from
linear stochastic system
D.
Computing population mean
and variance
E.
Monte Carlo simulation of
finite sample moments
PDF Backup
Concept A: State space form of Linear Difference
Equations.
Consider the state-space form
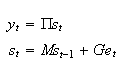
We
know from class that the difference equation ![]() can be
represented in this form as follows
can be
represented in this form as follows
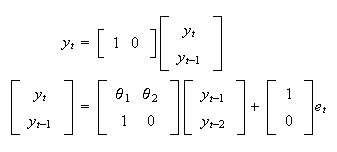
We also know from class that the state space form is convenient for many purposes, as will be illustrated below.
Problem 1: Write a Short MATLAB Program that sets up the
system above, creating the PI,G, and M matrices for specified values of theta (
![]() and
and ![]() .
.
Concept B: Stochastic simulation: a recursive
approach.
A
stochastic simulation in state space form is implemented recursively, as
follows. We begin by setting initial conditions ![]() , which implies
, which implies ![]() . Then, at date 1, we first draw a random
variable (in this case, a standard normal variable (N(0,1)) using randn.m). We
then update to get a new state.
. Then, at date 1, we first draw a random
variable (in this case, a standard normal variable (N(0,1)) using randn.m). We
then update to get a new state.
![]()
We next compute the y variable,
![]()
We
finally place the y variable in the vector ![]() , starting with
, starting with ![]()
![]()
Then,
we can restart the process from ![]() to
compute
to
compute ![]() and so
forth.
and so
forth.
Problem 2: Write a short program to stochastically simulate a y series, using the MATLAB built-in function randn.m (for information type "help randn") to generate a series of normal shocks.
Problem 3: change the simulation
so that the initial conditions are ![]() and show how the
simulation changes from the
and show how the
simulation changes from the ![]() simulation using the
same set of shocks in both cases.
simulation using the
same set of shocks in both cases.
Concept C: Impulse response.
The system impulse response is given by
![]()
It can be computed recursively.
Problem 4: Write a short program to compute the impulse response. The first few terms of the answer are: 1.0000, 1.3000, 1.2900, 1.1570, 0.9881.
Problem 5: Change the
![]() parameters so that
you have a set of complex roots. Graph the impulse response.
parameters so that
you have a set of complex roots. Graph the impulse response.
Concept D: Computing the population mean and
variance
There are a number of ways of computing population second moments for a state space system. One is to use the difference equation solution,
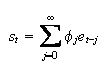
with the weights from the impulse response analysis above. Then, one can approximate the variance by using a large finite sum.
Another
way is to view the variance of the states, ![]() as
given by
as
given by
![]()
so that it is constrained by
![]()
Using
the column-stacking operator, ![]() , it will be the case that
, it will be the case that
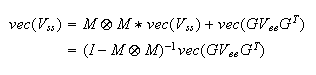
Problem 6: Write a program which implements these two methods.
Concept E: "Monte Carlo" analysis
This method can be used to study how finite sample means and variances are related to their population values. In such a simulation, one draws H samples of length T, computing the sample mean for each and the sample variance for each.
Problem 7: For H=1000 and T=100, conduct a Monte Carlo
analysis of the mean and variance of ![]() . Use the built-in
MATLAB function hist.m to display your results.
. Use the built-in
MATLAB function hist.m to display your results.