Wildman's
WeirdWildWeb
![]()
Electromagnetism and Maxwell’s Equations
Contents
The Equations
Notation and Definitions
Derivations of the Laws of Electrostatics and Magnetostatics
Equivalence of the Integral and Differential Forms of Maxwell’s Equations
![]()
The Equations
|
Electrostatics
and Magnetostatics |
Technology |
Maxwell’s
Equations |
|
|
Integral
Form |
Differential
Form |
||
|
Coulomb’s Law:
|
|
|
|
|
No Magnetic Monopoles |
|
|
|
|
Faraday’s Induction Law |
Dynamos and electromotors |
|
|
|
Ampere’s Law:
|
Electromagnets |
|
|
![]()
Notation and Definitions
![]() is the electric field.
is the electric field.
For every point (x,y,z,t) in spacetime, the
electric field specifies a vector (Ex(x,y,z,t),Ey(x,y,z,t),Ez(x,y,z,t)).
![]() is the magnetic field.
is the magnetic field.
For every point (x,y,z,t) in spacetime, the
magnetic field specifies a vector (Bx(x,y,z,t),By(x,y,z,t),Bz(x,y,z,t)).
![]() is the unit normal
vector to a surface, S;
is the unit normal
vector to a surface, S;
![]() is the unit tangent vector to
a curve, C.
is the unit tangent vector to
a curve, C.
Lorentz’s law of
force for electromagnetism specifies the force acting on a particle with
charge q and velocity v due to electric and magnetic fields
(it is akin to
![]() ):
):
![]() .
.
ε0 is the constant of permativity for the vacuum, which indicates how efficiently the electric field propogates through a vacuum.
μ0 is the constant of permeability for the vacuum, which indicates how efficiently the magnetic field propogates through a vacuum.
Coulomb’s Law presupposes a field-generating charge q1 and a test charge q2 separated by a distance r.
Ampere’s Law presupposes two parallel wires separated by a distance r carrying currents I1 and I2.
Current is related to
the current density
![]() as follows:
as follows:
![]() .
.
Charge is related to
the charge density
![]() as follows:
as follows:
![]() .
.
![]()
Derivations of the Laws of Electrostatics and Magnetostatics
1. Coulomb’s Law is a special case of Maxwell’s first equation. To see why, consider the integral form of Maxwell’s first equation and suppose that we apply it to the case of a field-generating charge q1 at the center of a sphere of radius r. The electric field, being spherically symmetric, will be constant everywhere on the sphere. Moreover, the electric field is radial so that its dot product with the normal vector at each point on the sphere will be simply its magnitude. So Maxwell’s first equation reduces in this case to:
![]() .
.
Recalling the formula for the surface area of a sphere, we have
![]() .
.
Using the fact that the electric field is in the radial direction, we may say that
![]() .
.
Finally, using the Lorentz force law for a test particle q2, we have
![]() ,
,
which is Coulomb’s Law.
2. Ampere’s Law is a special case of Maxwell’s fourth equation. To see why, consider the integral form of Maxwell’s fourth equation and suppose that we apply it to the case of parallel wires separated by a distance r carrying currents I1 and I2. We will take the current I1 to be the one that is generating the magnetic field whose integral around a circle of radius r we will calculate. Notice that the magnetic field is cylindrically symmetric and so is constant in magnitude everywhere on the circle around which we are to integrate and pointing always in the direction of the tangent. Knowing that there is no electric field in the picture, Maxwell’s fourth equation reduces to
![]() .
.
Recalling the circumference of a circle, we have
![]() .
.
The relevant part of the Lorentz force law in this case is
![]() ,
,
where the velocity is that of a charge moving through the second wire. Using the right-hand rule, we see that the direction of the cross product is the line perpendicular to the two wires, and the magnitude
![]() .
.
So, in this special arrangement, we have
![]() ,
,
which is Ampere’s Law.
![]()
Equivalence of the Integral and Differential Forms of Maxwell’s Equations
1. To understand the derivations of one form of Maxwell’s equations from the other form, it is necessary to know three important mathematics results. They are as follows.
a) For any vector field
![]() whose partial derivatives are
continuous, the Divergence Theorem (or Gauss’s Theorem) states that, in
colloquial terms, “whatever spread-apart-iness there is on the inside of
a volume, V, shows up as flux over the surface, S, of the volume.” More
precisely,
whose partial derivatives are
continuous, the Divergence Theorem (or Gauss’s Theorem) states that, in
colloquial terms, “whatever spread-apart-iness there is on the inside of
a volume, V, shows up as flux over the surface, S, of the volume.” More
precisely,
![]() .
.
The Divergence Theorem is useful for showing the equivalence of the integral and differential forms of Maxwell’s first and second equations.
b) For any vector field
![]() whose partial derivatives are
continuous, Stokes’ Theorem states that, in colloquial terms,
“whatever twistiness there is within a surface, S, shows up as an
overall twist (or circulation) on the border, C, of the surface.” More
precisely,
whose partial derivatives are
continuous, Stokes’ Theorem states that, in colloquial terms,
“whatever twistiness there is within a surface, S, shows up as an
overall twist (or circulation) on the border, C, of the surface.” More
precisely,
![]() .
.
Stokes’ Theorem is useful for showing the equivalence of the integral and differential forms of Maxwell’s third and fourth equations.
c) For sufficiently well behaved functions, it is possible to integrate and differentiate in either order.
2. Maxwell’s First Equation
a) Presupposing the differential form of Maxwell’s
first equation, how can we derive the integral form? Beginning with the
left-hand side of the integral form of Maxwell’s first equation, we
shall try to derive the right-hand side. The first step makes use of the
Divergence Theorem, the second step invokes the differential form of the
second equation, and the third step uses the relation between charge
density
![]() and charge:
and charge:
![]() .
.
b) In the reverse direction, presupposing the integral form of Maxwell’s first equation and using the Divergence Theorem again, consider that the equality
![]()
must hold for arbitrary volumes V. This can only occur if
![]() .
.
3. Maxwell’s Second Equation
a) Presupposing the differential form of Maxwell’s second equation, how can we derive the integral form? Beginning with the left-hand side of the integral form of Maxwell’s second equation, we shall try to derive the right-hand side. The first step makes use of the Divergence Theorem, the second step invokes the differential form of the second equation, and the third step is simple calculation:
![]() .
.
b) In the reverse direction, presupposing the integral form of Maxwell’s first equation and using the Divergence Theorem again, consider that the equality
![]()
must hold for arbitrary volumes V. This can only occur if
![]() .
.
4. Maxwell’s Third Equation
a) Presupposing the differential form of Maxwell’s third equation, how can we derive the integral form? Beginning with the left-hand side of the integral form of Maxwell’s third equation, we shall try to derive the right-hand side. The first step makes use of Stokes’ Theorem, the second step invokes the differential form of the fourth equation, and the third step reverses the order of differentiation and integration:
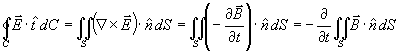
b) In the reverse direction, the derivation uses the same steps in a different order.
5. Maxwell’s Fourth Equation
a) Presupposing the differential form of Maxwell’s fourth equation, how can we derive the integral form? Beginning with the left-hand side of the integral form of Maxwell’s fourth equation, we shall try to derive the right-hand side. The first step makes use of Stokes’ Theorem, the second step invokes the differential form of the fourth equation, the third step is merely simplification, and the fourth step uses the definition of current, I, in terms of current density, J, and reverses the order of differentiation and integration:
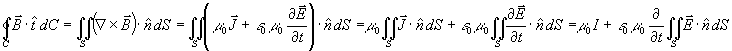
b) In the reverse direction, the derivation uses the same steps in a different order.
![]()
The information on this page is copyright ©1994-2010, Wesley Wildman (basic information here), unless otherwise noted. If you want to use ideas that you find here, please be careful to acknowledge this site as your source, and remember also to credit the original author of what you use, where that is applicable. If you want to use text or stories from these pages, please contact me at the feedback address for permission.
