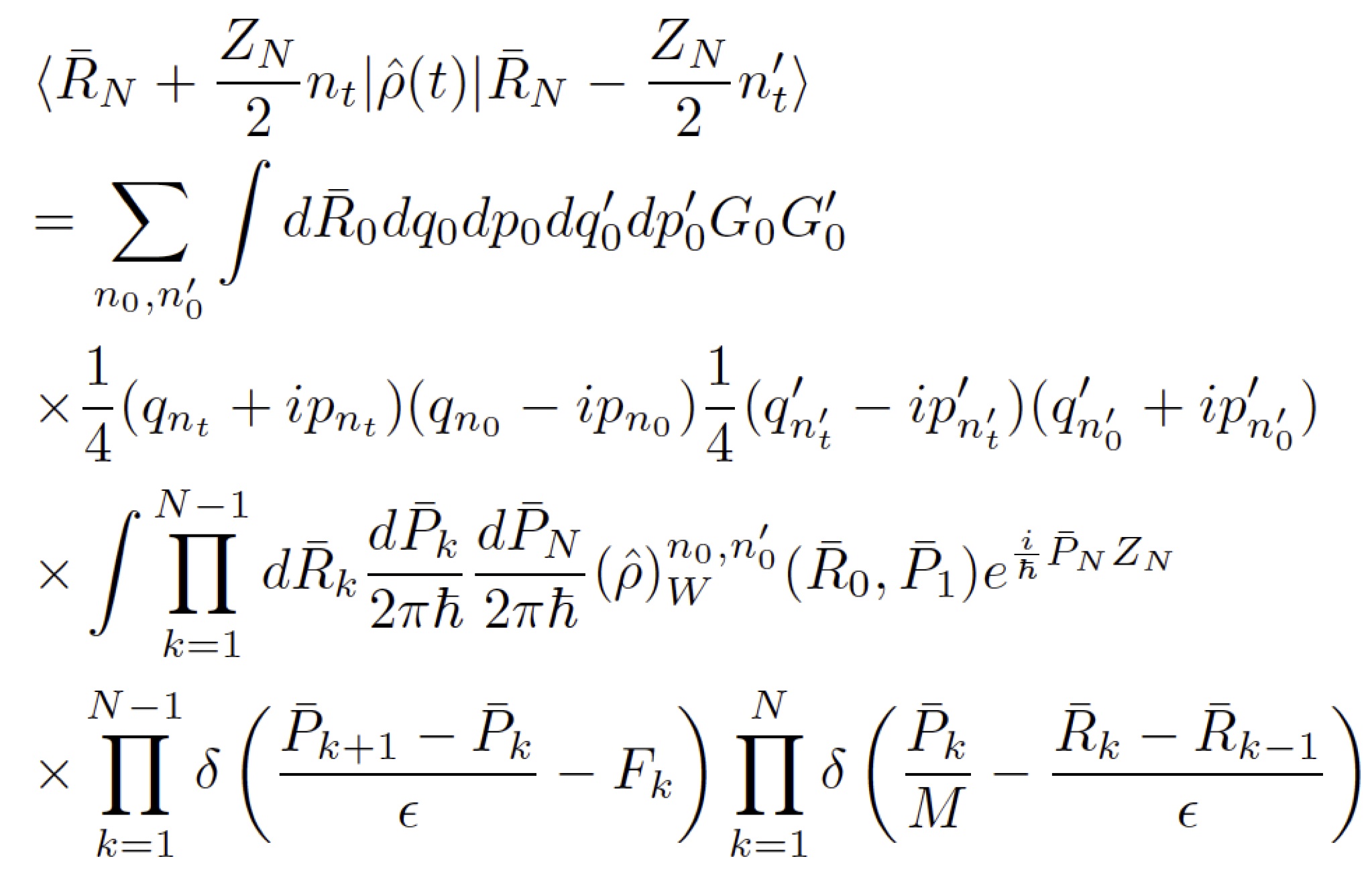
ALGORITHM DEVELOPMENT

The Coker group is interested in development of trajectory based theoretical approach to propagate the density matrix for a general class of systems described in terms of a quantum subsystem with discrete states that are coupled to a complex environment represented by continuous phase space degrees of freedom (DOF). Our most recently developed method, The Partial Linearized Density Matrix (PLDM) propagation method, accurately capture short time coherent behavior and also gives a reliable description of the relaxation to thermal equilibrium at long times. This has made the approach particularly useful for exploring realistic models of natural multi-chromophore photosynthetic light harvesting systems that show long lived coherence at early times and decoherence as equilibrium is approached in the long time limit. Another major advantage of our PLDM approach is the ability to treat arbitrary forms of system-bath coupling. Not only can the approach handle general non-linear coupling, but we also make no assumptions about the form of the spectral density that determines the frequency dependence of the system-bath coupling strength.

PHOTOSYNTHETIC ENERGY TRANSFER

We use our linearized quantum dynamics methods to explore the mechanisms underlying the fundamental processes by which natural photosynthetic light-harvesting systems transfer excitation energy through networks for chromophore molecules and feed this excitation into producing charge separation in reaction centers. The key general findings of this work explore how various characteristics of the different parts of the model hamiltonian influence the relaxation dynamics of these quantum dissipative networks as probed, for example, in non-linear spectroscopy experiments. Our most recent work presents some of the first detailed ab initio calculations of the spectral densities describing the different environments arising from chromophores in different regions of the protein support scaffolding and demonstrates that the heterogeneity of the spectral density can have a significant influence on the relaxation dynamics of these light harvesting systems.

ORGANIC PHOTOCHEMICAL REACTIONS

There have been significant recent advances in the development of organic synthetic methodology that make use of photo-activation of substrates for directed synthesis. Several important developments in this area have been pioneered by synthetic organic chemistry groups at Boston University (particularly the Porco group). Our group works to develop theoretical models and to study the mechanism underlying this important new excited state synthetic methodology. In particular, we developed a new genetic programming approach capable of fitting highly accurate and flexible reactive empirical valence bond (EVB) potential models using very limited ab initio single point energy data on these very large complex organic systems. This approach has been shown to be accurate and reliable, especially for treating solvent interaction effects on spectral line shapes. A cartesian reaction plane model for use in quantum dynamics calculations employing our PLDM propagation schemes has also been developed for analyzing high resolution matrix isolation spectra. Finally, our work extends new theoretical techniques like the string method for obtaining minimum energy paths on complex, high dimensional ab initio potential energy surfaces and the temperature accelerated molecular dynamics (TAMD) approach to map out the free energy surface and explore most probably reaction channels in condensed phase excited state reactive systems.

MATERIALS FOR PLASMONIC CATALYSIS