Electronic, vibrational, and rotational spectroscopy of molecules
 Spectroscopy is used to probe the dynamics and structure of molecules.
Spectroscopy is used to probe the dynamics and structure of molecules.
Ingredients: phenolphthalein, methylene blue
Procedure: A partial recipe follows.
1. Prepare a basic solution of phenolphthalein and potassium hydroxide.
2. Prepare an acidic solution of methylene blue and hydrochloric acid.
3. Present the two solutions for comparison and analyze in terms of the molecular structures of the indicators.
Understanding: Acid/base or reduction/oxidation indicators are typically organic molecules that undergo a change in charge state and electronic structure as solution conditions, such as the concentration of hydrogen ion, are varied.
Indicators can take on a wide range of colors. We observe a dramatic in color of phenolphthalein as the hydrogen ion concentration is lowered. At low pH, the phenolphthalein solution is colorless. At higher pH, the solution is pink to red. Methylene blue is a redox indicator that is blue in the presence of oxygen and becomes colorless when the concentration of oxygen is lowered. Can we understand these color changes in terms of the molecular structures of the indicators? Indeed we can!
Electronic spectroscopy as a probe of molecular structure
In studying the electronic configurations of atoms, the lowest energy electron configuration defines the ground electronic state. In the ground electronic state, there will be one or more atomic orbitals that are the highest energy occupied orbitals. The second lowest energy electron configuration is known as the first excited state.
For an atom in its ground electronic state, the lowest energy of transition is between the ground and first excited electronic states. That transition corresponds to the difference in energy between the highest occupied atomic orbital and the lowest unoccupied atomic orbital. An example is the transition in the hydrogen atom between the 1s (highest occupied) and 2s (lowest unoccupied) electronic configurations
ΔE = E2s - E1s
The same situation occurs when considering electronic transitions in molecules. The ground state configuration of electrons defines the Highest Occupied Molecular Orbital (HOMO) and Lowest Unoccupied Molecular Orbital (LUMO). The lowest energy electronic transition that is possible corresponds to exciting an electron in the HOMO to the LUMO, and the energy difference is
ΔE = ELUMO - EHOMO
For organic molecules with conjugated π systems of electrons, such as benzene, we can make the assumption that the lowest energy transition in the electronic state of the molecule will correspond to a π → π* transition, which we pronounce "π to π*" transition, with a corresponding energy
ΔE = Eπ* - Eπ
How can we understand the energy of a π → π* transition and how it varies from one molecule to the next? For example, if we consider a &pi → &pi* transition in benzene, will the corresponding &pi → &pi*
transition in naphthalene be higher or lower in energy? It turns out we can get a good idea by considering the energetics of the transition in terms of the particle-in-a-box model.
In our studies of molecular orbital theory, we have come to understand the electrons in σ bonding orbitals as being localized along the internuclear axis, between the bonding atoms. In π bonding orbitals, the electron density lies above and below the internuclear axis. When there are a number of alternating π and σ bonds, the molecular orbitals may be conjugated. That means that the local molecular orbitals can be combined to make supermolecular orbitals that extend over multiple bonds! The electrons that occupy those orbitals are delocalized.
It turns out that the energy of the π → π* transition depends upon the degree of delocalization of the electrons in the π system. We can make a good qualitative estimate of the trends using the particle-in-a-box model. You might say, "Hold on, man. There's no box!" Ah, but there is.
The conjugated π system extends some distance, and that distance is the length of the box, Lπ. The qualitative trend is that the difference between the ground and first excited state for the particle-in-a-box varies as
ΔE = 3h2/8mLπ2
Infrared (IR) spectroscopy probes the dynamics of molecular vibrations
We have seen how the allowed energies of the electrons in a one-electron atom, multielectron atoms, and molecules are quantized. Only certain energies are allowed, and each allowed energy state has a corresponding wavefunction that describes how the electrons are distributed around the atomic nuclei.
It turns out that vibrational and rotational motion of molecules is also quantized. For the vibrational motion, we think of the atomic nuclei moving on a potential surface that is determined by the ground electronic state - the lowest energy organization of the electrons around the nuclei. Considering the hydrogen chloride molecule, we can think of the H-Cl bond as a sort of "spring." The hydrogen and chlorine atoms are bonded together, and have an equilibrium bond length, req. There is a restoring force acting on the nuclei of the form
F = -k(r-req)
The frequency of oscillation of the bond is determined by (1) the force constant k that determines the magnitude of the restoring force on the bond and (2) the reduced mass of the molecule
μ=m1H m35Cl/(m1H +m35Cl)
ν=(1/2π)(k/μ)½
The quantized energies for the vibrations of the HCl molecule are simply
Ev=hν(v+½) v = 0, 1, 2...
This result is very interesting!
The transition energies available to the HCl "vibrator" will be multiples of hν. For a transition from the v vibrational quantum state to the v+1 vibrational quantum state, the transition energy is given by
ΔE=Ev+1 - Ev=hν
We note that the frequency of light that is absorbed or emitted in a transition between one vibrational quantum state and another is identical to the frequency of the electromagnetic radiation that induces the transition. Consider the case of the HCl molecule. The frequency of oscillation is 86.6 THz = 86.6x1012Hz (where 1 THz, pronounced "terahertz," is 1x1012Hz). As the reduced mass is μ=1.6269x10-27kg, the corresponding force constant for the HCl bond is found to be k=482 N/m (where 1 N = 1 kg m/s2).
The corresponding wavelength of light is 3,450nm which is solidly in the infrared region of the electromagnetic spectrum (700 nm < &lambdaIR < 105 nm).
These results tell us that in the vibrational ground state the HCl molecule oscillates roughly 87 times per picosecond, where a picosecond is 1x10-12s.
Or we can say that the HCl molecule oscillates 87 trillion times per second! This gives you a glimpse of the very great rate at which the events of the atomic and molecular world take place. That great rate of the dynamics at the atomic scale is necessary so that the dynamics of our lives can occur on the much slower time scale of milliseconds and beyond.
Microwave (μ-wave) spectroscopy probes the dynamics of molecular rotations
We have found that the electronic states of atoms and molecules are quantized, and that the vibrational states of molecules are quantized. It will come as no surprise that the rotational states of molecules are also quantized.
It can be shown that the allowed quantum mechanical energies of a rotating molecule such as HCl are given by
EJ=J(J+1) h2/(8π2I) J = 0, 1, 2...
I=μ req2
Let's determine the allowed transition energies of the quantized HCl "rotator." For a transition from the J quantum state to the J+1 quantum state, the transition energy is given by
ΔE=EJ+1 - EJ=2hB(J+1)
B = h/(8π2I)
There is something else that is different about transitions between rotational quantum states. The rotational splitting
is dependent on the molecular structure! The moment of inertia depends upon the reduced mass and the equilibrium bond length.
I = h/(8π2B)
For HCl we find experimentally that 2B=0.623 THz = 0.623x1012Hz. That implies that the moment of inertia of the HCl molecule is I=2.69x10-47kg m2. From the moment of inertia and a knowledge of the reduced mass, we find that the equilibrium bond length of the HCl molecule is req=1.29x10-10m=1.29Å. The transition frequency corresponds to a wavelength of 480 μm which is solidly in the microwave region of the electromagnetic spectrum (105 nm < λμ-wave < 108 nm).
The take home message is that μ-wave spectroscopy can be used to determine information about molecular dynamics and structure. Much of what is now known about the structure of small molecules was first determined using μ-wave spectroscopy.
Assume that the λmax is associated with the HOMO to LUMO transition in the π electron system of the dye molecule. In each case, use the particle-in-a-box model to estimate the length of the conjugated π system by computing the length of the "box." Assume that there is only one electron in your box. Compare your results with the molecular structures of the three dye molecules. Do your answers make physical sense?
Compare your results with the results of the multielectron particle-in-a-box model used to interpret your laboratory data for the same molecules. Which approximation, the one or multiple electron model, leads to the most accurate results?
You can check your answers here.
You can check your answers here.
The infrared spectrum of isotopically labeled formic acid, H13COOH, is also analyzed. Is the C=O stretching frequency blue shifted, to higher frequency, or red shifted, to lower frequency, due to the isotopic labeling?
You can check your answers here.
You can check your answers here.
Exploring the colors of dyes using the particle-in-a-box model
Question:
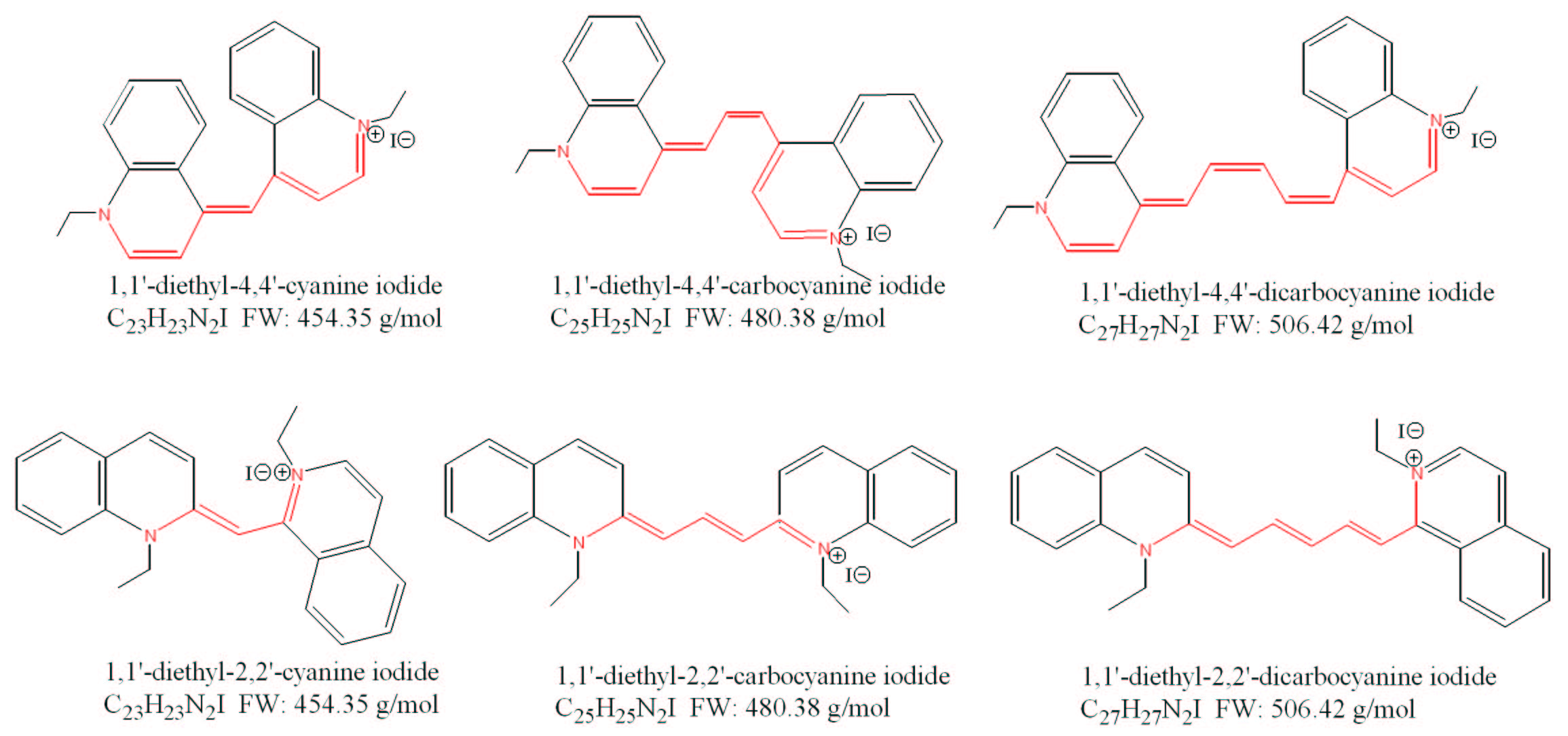
The dyes cyanine (1,1'-diethyl-4,4'-cyanine iodide), pinacyanol (1,1'-diethyl-4,4'-carbocyanine iodide), and dicarbocyanine (1,1'-diethyl-4,4'-dicarbocyanine iodide) have distinct molecular structures and associated colors. The wavelength of maximum absorption in the electronic spectrum, λmax, can be related to the apparent color of the dye. The dye cyanine has a λmax=523 nm and it appears red. The dye carbocyanine has a λmax=604 nm and it appears bluish-purple, while dicarbocyanine has a λmax=706 nm and appears green.
Assigning the infrared spectrum of a mixture of gases
Question:
A gaseous mixture of HBr and HI is analyzed.
The IR spectrum of the gaseous mixtures displays two absorption lines at distinct frequencies, 7.68 x 1013 Hz and 6.69 x 1013 Hz.
Assume that the absorption lines correspond to transitions between the ground and first excited vibrational quantum states in each of the molecules.
Assign each absorption line in the IR spectrum to the vibrational transition of either HI or HBr.
Assigning the infrared spectrum of a small organic molecule
Question:
An infrared spectrum of formic acid, H12COOH, is analyzed. The C=O stretching vibration is found to occur at 1777 cm-1. The funny unit cm-1 is called the wavenumber; it is the frequency of the vibration in Hertz, divided by the speed of light, 2.99 x 1010 cm/s.
Assigning the microwave spectrum of a mixture of gases
Question:
The pure rotational spectrum of 1H35Cl displays a splitting between the ground and first excited rotational states that is consistent with a rotational constant B=0.312 x 1012 Hz. You are asked to analyze the rotational spectrum of 2H35Cl, also known as deuterated HCl, "heavy" HCl, deuterium-labeled HCl, or DCl. Assume that the bond lengths of DCl and HCl are the same. Predict the frequency of transition between the ground and first excited rotational states of DCl.