Plotting information on the eigenvalues of a matrix

Plotting information on the eigenvalues of a matrix

Samuelson's chart 2 helps us understand the behavior of his model economy, by displaying combinations of parameters for which the solution contains: (i) real or complex components; and (ii) stable or unstable components.

His dynamic model is

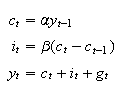
which can be cast in state-space form,

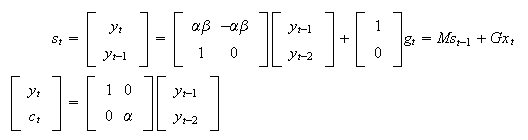
with an identity being used to determine .

The program samuelson.m shows how to determine the eigenvalues of this model, as well as drawing chart 2 from Samuelson's paper. In a more complicated model, it might not be possible to analytically determine how various parameter values led to qualitative behavior, but a similar computational and graphical approach could be used to view the implications of alternative parameter values.

% samuelson.m

Comments

% Program Component 1: Find Roots of

% System for specific parameter values

% Specify parameters

alph=.5;

bet=1.6;

% Implied parameters

theta1=alph*(1+bet);

theta2=-alph*bet;

% Define a matrix M which has the necessary form

M = [theta1 theta2

1 0];

% Calculate eigenvalues

mu=eig(M);

% Calculate roots of z2 - theta1*z - theta2 = 0

mualt=roots([1 -theta1 -theta2]);

disp('Roots of Samuelson model')

disp([mu mualt])

disp(' ')

disp('strike any key to continue')

pause

% Program component 2

% Draw Samuelson's chart

inc=.2;

alphv=.1:inc:.9;

betv=.1:inc:5;

RTAB=zeros(length(alphv),length(betv));

STAB=zeros(length(alphv),length(betv));

for i=1:length(alphv);

for j=1:length(betv);

alph=alphv(i);

bet=betv(j);

% Implied parameters

theta1=alph*(1+bet);

theta2=-alph*bet;

% Calculate roots of z2 - theta1*z - theta2 = 0

mualt=roots([1 -theta1 -theta2]);

% make table with 1 if roots are complex

iscomplex=(1-isreal(mualt));

RTAB(i,j)=iscomplex;

% make table with 1 if roots are stable

isunstable=(1-(max(abs(mualt))<1));

STAB(i,j)=isunstable;

end

betvs=1:inc:5;

line1=ones(size(betvs))./betvs;

line2=4*betv./((1+betv).2);

% plot Samuelson's curves

axis([0 5 0 1])

plot(betvs,line1,'-k',betv,line2,'-')

hold on

% plot roots characteristics as points, excluding those where there is a

% zero in either table

for i=1:length(alphv);

getr=RTAB(i,:)>0;

gets=STAB(i,:)>0;

plot(betv(getr),alphv(i)*ones(sum(getr)),'ok',…

betv(gets),alphv(i)*ones(sum(gets)),'*k')

end

title('Samuelson chart 2')