Defining a function file: Exponential smoothing filter example

Defining a function file: Exponential smoothing filter example

The programming problem associated with the exponential smoothing filter is

where is the value of the series at date t and is the growth component extracted by the filter. The first-order conditions for an interior solution to this problem are:

for each , and

These may be viewed as a matrix system

with and being column vectors of size .

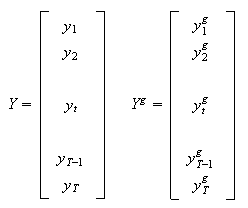
with

The following function file constructs this matrix, taking in a vector and creating a vector , which is called "g" in the program.

esmf.m

% applies the "Exponential Smoothing" filter to time series

% using a matrix inversion technique. The data is assumed to be

% organized into a matrix "y" with the rows of y

% being the observations and the columns being the series.

% The value of the smoothing parameter is the second argument.

% The output is the filtered series g.

function g=esmf(y,lam)

% ESM filtering involves the solution of the difference equation:

% y(t) = - lam*g(t+1)

+ (1+2*lam)*g(t) -lam*g(t-1)

% with

% y(1) = (1+lambda)*g(1) - lam*g(2)

% y(T) = (1+lambda)*g(T) - lam*g(T-1)

% If there are a smaller number of observations than series, then

% there is most likely a mistake: convert the vector/matrix of inputs:

oy = size(y);

ny = max(oy); % length of time series

if (oy(1)<oy(2))

y=y';

end

disp('Computing Exponential Smoothing Filtered Time Series with Matrix Inversion')

disp('Growth Component is Returned as g')

% Strategy: Structure difference equation as a matrix equation:

% M g = y

% and then invert M.

M = zeros(ny,ny);

d1=ones(ny-1,1);

d1=-d1*lam;

d2=ones(ny,1);

d2=d2*(1+2*lam);

d2(1)=1+lam;

d2(ny)=1+lam;

M = diag(d1,1)+diag(d2)+diag(d1,-1);

g = inv(M)*y;

% convert if necessary

if (oy(1)<oy(2))

g=g';

end

This program makes use of the built-in MATLAB function diag, to build the block diagonal matrix M. diag(x) puts the vector x on the main diagonal; diag(z,1) puts the vector z on the "subdiagonal"; diag(x,-1) puts the vector z on the "superdiagonal". z must be one element shorter than x, as in the code.